|
让转化思想在学生的思维中生根
转化是一种很重要的数学思想,一般指对于直接求解比较困难的问题,通过观察、分析、类比、联想等思维过程,选择恰当的数学方法,将原问题转化为一个简单、容易理解的新问题,从而达到求解的目的。转化思想给数学的学习注入了新的灵魂,特别是对于小学生来说,了解、掌握和运用“转化”的数学思想与方法,可以提高数学学习的效率,培养数学思维,提高数学应用意识。因此,我们在教学中要对所教的内容融合贯通,突破定势思维,有意识的引导学生运用转化思想。那么转化思想在数学中的应用有哪些呢?
一.化新为旧
任何一个新知识,都是在原有知识发展和转化的结果。在我们的教学中,我们可以给新知识找到一个合适的生长点,把学生感到不熟悉的问题转化成熟悉的问题,引导学生运用原有的知识经验去解决问题。例如,在进行异分母分数加减法教学时。我们可以这样做:学生学习了同分母分数加、减法的计算方法,那我们就可以在学生原有知识的基础上,提问问题:异分母分数加法怎样计算,让学生进行新旧知识的对比。接下来,给学生提供探究的平台,让学生自己去观察、思考、交流,把新知识转化成已学过的旧知识,教师适时引导,让学生大胆推理,并进行验证,得出结论。通过转化,让学生能够更好的理解新知,达到知识迁移的目的。
二.化不规则为规则
在数学中,对于长方体、正方体、圆柱这些规则的图形,我们可以用公式轻而易举地求出他们的面积。但是在生活中,我们经常会遇到不规则的东西,比如土豆、西红柿等,那么我们应该如何求出它们的面积呢?这个时候就更加体现了转化思想的重要性。我们可以引导学生通过自主合作探究活动,寻找自己认为合适的转化方法,我们适时地参与、倾听、指导。我们可以选择一个长方体或正方体容器加满水,通过测量它的长、宽、高,计算出它的容积,然后把土豆放进容器里,排出一些水,可以用量筒接住这些水,看看水的体积是多少,就直接得出了土豆的体积;如果不方便接水,可以把土豆从容器中取出来,量一量容器上方空出的体积是多少,这就是土豆的体积了。通过将不规则的图形转化为规则整齐的图形,从而计算出物体的体积,使我们生活中的问题迎刃而解。
三.化曲为直
“化曲为直”的转化思想可以打破学生的空间障碍,把思想引向更宽更广的层次。它在小学数学曲面图形的学习中运用非常多。比如:我们学习了长方体的体积,那么在学习圆柱体的体积时,可以通过将圆柱沿着底面半径平均分成若干等份,拼接成一个长方形来实现转化。还有《圆的面积》教学,在教学过程中,可以引导学生用半径把圆平均分成若干等分以,拼成近似的长方形,长方形的长就相当于圆周长的一半,长方形的宽就相当于圆的半径,由此用长方形的面积公式长乘宽就可以推导出圆的面积。通过“化曲为直”将新旧知识也联系了起来,既学了知识,又掌握了方法。 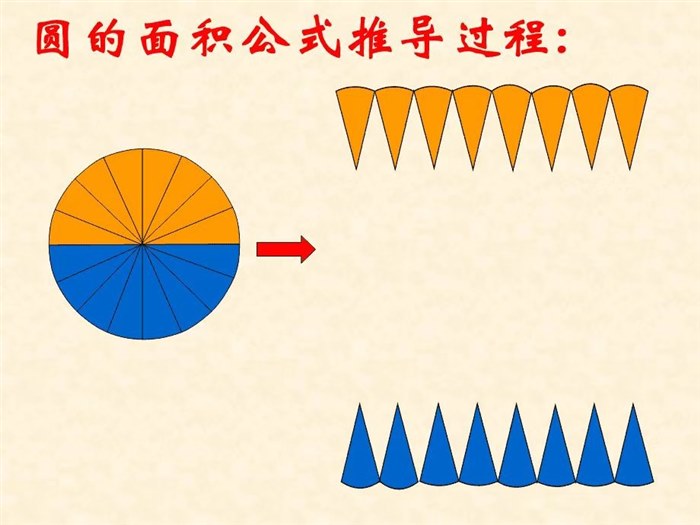
四.化繁为简 有些题目比较复杂,学生如果只是一味地“看题”思考,不一定能发现其中的数量关系,如果想使问题简单化,我们可以尝试用用一些方法,比如画图。例如经典的握手问题:“小明、小丽、小华第一次见面,非常高兴相互握手表示友好,想一想, 如果每两个小朋友握一次手,每个人都要握到,他们一共要握几次手?”初次见到这种题目,学生可能会无从下手,这个时候,我们就可以引导学生尝试画图解决,通过画图分析,我们可以很直观地得出答案。这样一来不但可以化繁为简,而且更容易激发学生的学习兴趣。 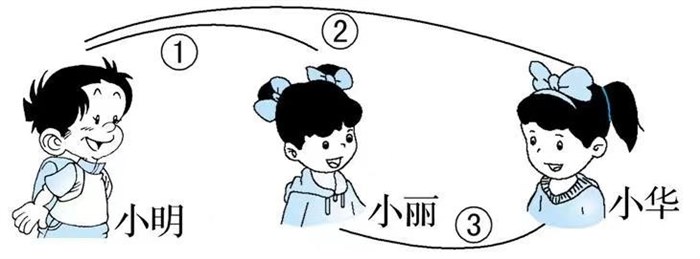 总之,转化思想是解决数学问题的基本思路和途径之一,是一种重要的数学思想方法。作为数学老师,我们在教学时,应该结合相应的数学情景,培养学生利用转化思想解决问题的意识。让转化思想成为小学生学习与思考重要法宝。 |